Skip to content
Permalink
master
Switch branches/tags

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

ME3255S2017/lecture_13/lecture_13.md

Go to file
 
 
Cannot retrieve contributors at this time
962 lines (624 sloc) 17.4 KB
Raw Blame
Open in GitHub Desktop
```octave
%plot --format svg
```
```octave
setdefaults
```
## My question from last class
![q1](efficient_soln.png)
![A](https://lh4.googleusercontent.com/fmG7EnFxpvvjSgijOuwz8osuiH3cBDgOzTE64KnfQeeDDSG2oE86-BzcpYIQMVkkAgRRGEDEGi6-Nkr8qmEMeaAk-gcjEmXe42WFYUdOa5XoUaBkXRakkA77_XrkRjArCGZIFhjjDRoO7x0)
![q2](norm_A.png)
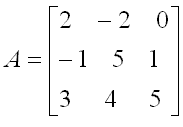## Your questions from last class
1. Do we have to submit a link for HW #4 somewhere or is uploading to Github sufficient?
-no, your submission from HW 3 is sufficient
2. How do I get the formulas/formatting in markdown files to show up on github?
-no luck for markdown equations in github, this is an ongoing request
3. Confused about the p=1 norm part and ||A||_1
4. When's the exam?
-next week (3/9)
5. What do you recommend doing to get better at figuring out the homeworks?
-time and experimenting (try going through the lecture examples, verify my work)
6. Could we have an hw or extra credit with a video lecture to learn some simple python?
-Sounds great! how simple?
-[Installing Python and Jupyter Notebook (via Anaconda) - https://www.continuum.io/downloads](https://www.continuum.io/downloads)
-[Running Matlab kernel in Jupyter - https://anneurai.net/2015/11/12/matlab-based-ipython-notebooks/](https://anneurai.net/2015/11/12/matlab-based-ipython-notebooks/)
-[Running Octave kernel in Jupyter - https://anaconda.org/pypi/octave_kernel](https://anaconda.org/pypi/octave_kernel)
# Markdown examples
` " ' ` `
```matlab
x=linspace(0,1);
y=x.^2;
plot(x,y)
for i = 1:10
fprintf('markdown is pretty')
end
```
## Condition of a matrix
### *just checked in to see what condition my condition was in*
### Matrix norms
The Euclidean norm of a vector is measure of the magnitude (in 3D this would be: $|x|=\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}$) in general the equation is:
$||x||_{e}=\sqrt{\sum_{i=1}^{n}x_{i}^{2}}$
For a matrix, A, the same norm is called the Frobenius norm:
$||A||_{f}=\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{m}A_{i,j}^{2}}$
In general we can calculate any $p$-norm where
$||A||_{p}=\sqrt{\sum_{i=1}^{n}\sum_{i=1}^{m}A_{i,j}^{p}}$
so the p=1, 1-norm is
$||A||_{1}=\sqrt{\sum_{i=1}^{n}\sum_{i=1}^{m}A_{i,j}^{1}}=\sum_{i=1}^{n}\sum_{i=1}^{m}|A_{i,j}|$
$||A||_{\infty}=\sqrt{\sum_{i=1}^{n}\sum_{i=1}^{m}A_{i,j}^{\infty}}=\max_{1\le i \le n}\sum_{j=1}^{m}|A_{i,j}|$
### Condition of Matrix
The matrix condition is the product of
$Cond(A) = ||A||\cdot||A^{-1}||$
So each norm will have a different condition number, but the limit is $Cond(A)\ge 1$
An estimate of the rounding error is based on the condition of A:
$\frac{||\Delta x||}{x} \le Cond(A) \frac{||\Delta A||}{||A||}$
So if the coefficients of A have accuracy to $10^{-t}
and the condition of A, $Cond(A)=10^{c}$
then the solution for x can have rounding errors up to $10^{c-t}$
```octave
A=[1,1/2,1/3;1/2,1/3,1/4;1/3,1/4,1/5]
[L,U]=LU_naive(A)
```
A =
1.00000 0.50000 0.33333
0.50000 0.33333 0.25000
0.33333 0.25000 0.20000
L =
1.00000 0.00000 0.00000
0.50000 1.00000 0.00000
0.33333 1.00000 1.00000
U =
1.00000 0.50000 0.33333
0.00000 0.08333 0.08333
0.00000 -0.00000 0.00556
Then, $A^{-1}=(LU)^{-1}=U^{-1}L^{-1}$
$Ld_{1}=\left[\begin{array}{c}
1 \\
0 \\
0 \end{array}\right]$, $Ux_{1}=d_{1}$ ...
```octave
invA=zeros(3,3);
d1=L\[1;0;0];
d2=L\[0;1;0];
d3=L\[0;0;1];
invA(:,1)=U\d1; % shortcut invA(:,1)=A\[1;0;0]
invA(:,2)=U\d2;
invA(:,3)=U\d3
invA*A
```
invA =
9.0000 -36.0000 30.0000
-36.0000 192.0000 -180.0000
30.0000 -180.0000 180.0000
ans =
1.0000e+00 3.5527e-15 2.9976e-15
-1.3249e-14 1.0000e+00 -9.1038e-15
8.5117e-15 7.1054e-15 1.0000e+00
Find the condition of A, $cond(A)$
```octave
% Frobenius norm
normf_A = sqrt(sum(sum(A.^2)))
normf_invA = sqrt(sum(sum(invA.^2)))
cond_f_A = normf_A*normf_invA
norm(A,'fro')
% p=1, column sum norm
norm1_A = max(sum(A,2))
norm1_invA = max(sum(invA,2))
norm(A,1)
cond_1_A=norm1_A*norm1_invA
% p=inf, row sum norm
norminf_A = max(sum(A,1))
norminf_invA = max(sum(invA,1))
norm(A,inf)
cond_inf_A=norminf_A*norminf_invA
```
normf_A = 1.4136
normf_invA = 372.21
cond_f_A = 526.16
ans = 1.4136
norm1_A = 1.8333
norm1_invA = 30.000
ans = 1.8333
cond_1_A = 55.000
norminf_A = 1.8333
norminf_invA = 30.000
ans = 1.8333
cond_inf_A = 55.000
Consider the problem again from the intro to Linear Algebra, 4 masses are connected in series to 4 springs with spring constants $K_{i}$. What does a high condition number mean for this problem?
![Springs-masses](../lecture_09/mass_springs.png)
The masses haves the following amounts, 1, 2, 3, and 4 kg for masses 1-4. Using a FBD for each mass:
$m_{1}g+k_{2}(x_{2}-x_{1})-k_{1}x_{1}=0$
$m_{2}g+k_{3}(x_{3}-x_{2})-k_{2}(x_{2}-x_{1})=0$
$m_{3}g+k_{4}(x_{4}-x_{3})-k_{3}(x_{3}-x_{2})=0$
$m_{4}g-k_{4}(x_{4}-x_{3})=0$
in matrix form:
$\left[ \begin{array}{cccc}
k_{1}+k_{2} & -k_{2} & 0 & 0 \\
-k_{2} & k_{2}+k_{3} & -k_{3} & 0 \\
0 & -k_{3} & k_{3}+k_{4} & -k_{4} \\
0 & 0 & -k_{4} & k_{4} \end{array} \right]
\left[ \begin{array}{c}
x_{1} \\
x_{2} \\
x_{3} \\
x_{4} \end{array} \right]=
\left[ \begin{array}{c}
m_{1}g \\
m_{2}g \\
m_{3}g \\
m_{4}g \end{array} \right]$
```octave
k1=10; % N/m
k2=100000;
k3=10;
k4=1;
m1=1; % kg
m2=2;
m3=3;
m4=4;
g=9.81; % m/s^2
K=[k1+k2 -k2 0 0; -k2 k2+k3 -k3 0; 0 -k3 k3+k4 -k4; 0 0 -k4 k4]
y=[m1*g;m2*g;m3*g;m4*g]
```
K =
100010 -100000 0 0
-100000 100010 -10 0
0 -10 11 -1
0 0 -1 1
y =
9.8100
19.6200
29.4300
39.2400
```octave
cond(K,inf)
cond(K,1)
cond(K,'fro')
cond(K,2)
```
ans = 3.2004e+05
ans = 3.2004e+05
ans = 2.5925e+05
ans = 2.5293e+05
```octave
e=eig(K)
max(e)/min(e)
```
e =
7.9078e-01
3.5881e+00
1.7621e+01
2.0001e+05
ans = 2.5293e+05
## P=2 norm is ratio of biggest eigenvalue to smallest eigenvalue!
no need to calculate the inv(K)
# Iterative Methods
## Gauss-Seidel method
If we have an intial guess for each value of a vector $x$ that we are trying to solve, then it is easy enough to solve for one component given the others.
Take a 3$\times$3 matrix
$Ax=b$
$\left[ \begin{array}{ccc}
3 & -0.1 & -0.2 \\
0.1 & 7 & -0.3 \\
0.3 & -0.2 & 10 \end{array} \right]
\left[ \begin{array}{c}
x_{1} \\
x_{2} \\
x_{3} \end{array} \right]=
\left[ \begin{array}{c}
7.85 \\
-19.3 \\
71.4\end{array} \right]$
$x_{1}=\frac{7.85+0.1x_{2}+0.2x_{3}}{3}$
$x_{2}=\frac{-19.3-0.1x_{1}+0.3x_{3}}{7}$
$x_{3}=\frac{71.4+0.1x_{1}+0.2x_{2}}{10}$
```octave
A=[3 -0.1 -0.2;0.1 7 -0.3;0.3 -0.2 10]
b=[7.85;-19.3;71.4]
x=A\b
```
A =
3.00000 -0.10000 -0.20000
0.10000 7.00000 -0.30000
0.30000 -0.20000 10.00000
b =
7.8500
-19.3000
71.4000
x =
3.0000
-2.5000
7.0000
### Gauss-Seidel Iterative approach
As a first guess, we can use $x_{1}=x_{2}=x_{3}=0$
$x_{1}=\frac{7.85+0.1(0)+0.3(0)}{3}=2.6167$
$x_{2}=\frac{-19.3-0.1(2.6167)+0.3(0)}{7}=-2.7945$
$x_{3}=\frac{71.4+0.1(2.6167)+0.2(-2.7945)}{10}=7.0056$
Then, we update the guess:
$x_{1}=\frac{7.85+0.1(-2.7945)+0.3(7.0056)}{3}=2.9906$
$x_{2}=\frac{-19.3-0.1(2.9906)+0.3(7.0056)}{7}=-2.4996$
$x_{3}=\frac{71.4+0.1(2.9906)+0.2(-2.4966)}{10}=7.00029$
The results are conveerging to the solution we found with `\` of $x_{1}=3,~x_{2}=-2.5,~x_{3}=7$
We could also use an iterative method that solves for all of the x-components in one step:
### Jacobi method
$x_{1}^{i}=\frac{7.85+0.1x_{2}^{i-1}+0.3x_{3}^{i-1}}{3}$
$x_{2}^{i}=\frac{-19.3-0.1x_{1}^{i-1}+0.3x_{3}^{i-1}}{7}$
$x_{3}^{i}=\frac{71.4+0.1x_{1}^{i-1}+0.2x_{2}^{i-1}}{10}$
Here the solution is a matrix multiplication and vector addition
$\left[ \begin{array}{c}
x_{1}^{i} \\
x_{2}^{i} \\
x_{3}^{i} \end{array} \right]=
\left[ \begin{array}{c}
7.85/3 \\
-19.3/7 \\
71.4/10\end{array} \right]-
\left[ \begin{array}{ccc}
0 & 0.1/3 & 0.2/3 \\
0.1/7 & 0 & -0.3/7 \\
0.3/10 & -0.2/10 & 0 \end{array} \right]
\left[ \begin{array}{c}
x_{1}^{i-1} \\
x_{2}^{i-1} \\
x_{3}^{i-1} \end{array} \right]$
|x_{j}|Jacobi method |vs| Gauss-Seidel |
|--------|------------------------------|---|-------------------------------|
|$x_{1}^{i}=$ | $\frac{7.85+0.1x_{2}^{i-1}+0.3x_{3}^{i-1}}{3}$ | | $\frac{7.85+0.1x_{2}^{i-1}+0.3x_{3}^{i-1}}{3}$|
|$x_{2}^{i}=$ | $\frac{-19.3-0.1x_{1}^{i-1}+0.3x_{3}^{i-1}}{7}$ | | $\frac{-19.3-0.1x_{1}^{i}+0.3x_{3}^{i-1}}{7}$ |
|$x_{3}^{i}=$ | $\frac{71.4+0.1x_{1}^{i-1}+0.2x_{2}^{i-1}}{10}$ | | $\frac{71.4+0.1x_{1}^{i}+0.2x_{2}^{i}}{10}$|
```octave
ba=b./diag(A) % or ba=b./[A(1,1);A(2,2);A(3,3)]
sA=A-diag(diag(A)) % A with zeros on diagonal
sA(1,:)=sA(1,:)/A(1,1);
sA(2,:)=sA(2,:)/A(2,2);
sA(3,:)=sA(3,:)/A(3,3)
x0=[0;0;0];
x1=ba-sA*x0
x2=ba-sA*x1
x3=ba-sA*x2
fprintf('solution is converging to [3,-2.5,7]]\n')
```
ba =
2.6167
-2.7571
7.1400
sA =
0.00000 -0.10000 -0.20000
0.10000 0.00000 -0.30000
0.30000 -0.20000 0.00000
sA =
0.000000 -0.033333 -0.066667
0.014286 0.000000 -0.042857
0.030000 -0.020000 0.000000
x1 =
2.6167
-2.7571
7.1400
x2 =
3.0008
-2.4885
7.0064
x3 =
3.0008
-2.4997
7.0002
solution is converging to [3,-2.5,7]]
```octave
diag(A)
diag(diag(A))
```
ans =
3
7
10
ans =
Diagonal Matrix
3 0 0
0 7 0
0 0 10
This method works if problem is diagonally dominant,
$|a_{ii}|>\sum_{j=1,j\ne i}^{n}|a_{ij}|$
If this condition is true, then Jacobi or Gauss-Seidel should converge
```octave
A=[0.1,1,3;1,0.2,3;5,2,0.3]
b=[12;2;4]
A\b
```
A =
0.10000 1.00000 3.00000
1.00000 0.20000 3.00000
5.00000 2.00000 0.30000
b =
12
2
4
ans =
-2.9393
9.1933
1.0336
```octave
ba=b./diag(A) % or ba=b./[A(1,1);A(2,2);A(3,3)]
sA=A-diag(diag(A)) % A with zeros on diagonal
sA(1,:)=sA(1,:)/A(1,1);
sA(2,:)=sA(2,:)/A(2,2);
sA(3,:)=sA(3,:)/A(3,3)
x0=[0;0;0];
x1=ba-sA*x0
x2=ba-sA*x1
x3=ba-sA*x2
fprintf('solution is not converging to [-2.93,9.19,1.03]\n')
```
ba =
120.000
10.000
13.333
sA =
0 1 3
1 0 3
5 2 0
sA =
0.00000 10.00000 30.00000
5.00000 0.00000 15.00000
16.66667 6.66667 0.00000
x1 =
120.000
10.000
13.333
x2 =
-380.00
-790.00
-2053.33
x3 =
6.9620e+04
3.2710e+04
1.1613e+04
solution is not converging to [-2.93,9.19,1.03]
## Gauss-Seidel with Relaxation
In order to force the solution to converge faster, we can introduce a relaxation term $\lambda$.
where the new x values are weighted between the old and new:
$x^{i}=\lambda x^{i}+(1-\lambda)x^{i-1}$
after solving for x, lambda weights the current approximation with the previous approximation for the updated x
```octave
% rearrange A and b
A=[3 -0.1 -0.2;0.1 7 -0.3;0.3 -0.2 10]
b=[7.85;-19.3;71.4]
iters=zeros(100,1);
for i=1:100
lambda=2/100*i;
[x,ea,iters(i)]=Jacobi_rel(A,b,lambda);
end
plot([1:100]*2/100,iters)
```
A =
3.00000 -0.10000 -0.20000
0.10000 7.00000 -0.30000
0.30000 -0.20000 10.00000
b =
7.8500
-19.3000
71.4000
![svg](lecture_13_files/lecture_13_24_1.svg)
```octave
l=fminbnd(@(l) lambda_fcn(A,b,l),0.5,1.5)
```
l = 0.99158
```octave
A\b
```
ans =
3.0000
-2.5000
7.0000
```octave
[x,ea,iter]=Jacobi_rel(A,b,l,0.000001)
[x,ea,iter]=Jacobi_rel(A,b,1,0.000001)
```
x =
3.0000
-2.5000
7.0000
ea =
1.8289e-07
2.1984e-08
2.3864e-08
iter = 8
x =
3.0000
-2.5000
7.0000
ea =
1.9130e-08
7.6449e-08
3.3378e-08
iter = 8
## Nonlinear Systems
Consider two simultaneous nonlinear equations with two unknowns:
$x_{1}^{2}+x_{1}x_{2}=10$
$x_{2}+3x_{1}x_{2}^{2}=57$
Graphically, we are looking for the solution:
```octave
x11=linspace(0.5,3);
x12=(10-x11.^2)./x11;
x22=linspace(2,8);
x21=(57-x22).*x22.^-2/3;
plot(x11,x12,x21,x22)
% Solution at x_1=2, x_2=3
hold on;
plot(2,3,'o')
xlabel('x_1')
ylabel('x_2')
```
![svg](lecture_13_files/lecture_13_29_0.svg)
## Newton-Raphson part II
Remember the first order approximation for the next point in a function is:
$f(x_{i+1})=f(x_{i})+(x_{i+1}-x_{i})f'(x_{i})$
then, $f(x_{i+1})=0$ so we are left with:
$x_{i+1}=x_{i}-\frac{f(x_{i})}{f'(x_{i})}$
We can use the same formula, but now we have multiple dimensions so we need to determine the Jacobian
$[J]=\left[ \begin{array}{cccc}
\frac{\partial f_{1,i}}{\partial x_{1}} & \frac{\partial f_{1,i}}{\partial x_{2}} &
\cdots & \frac{\partial f_{1,i}}{\partial x_{n}} \\
\frac{\partial f_{2,i}}{\partial x_{1}} & \frac{\partial f_{2,i}}{\partial x_{2}} &
\cdots & \frac{\partial f_{2,i}}{\partial x_{n}} \\
\vdots & \vdots & & \vdots \\
\frac{\partial f_{n,i}}{\partial x_{1}} & \frac{\partial f_{n,i}}{\partial x_{2}} &
\cdots & \frac{\partial f_{n,i}}{\partial x_{n}} \\
\end{array} \right]$
$\left[ \begin{array}{c}
f_{1,i+1} \\
f_{2,i+1} \\
\vdots \\
f_{n,i+1}\end{array} \right]=
\left[ \begin{array}{c}
f_{1,i} \\
f_{2,i} \\
\vdots \\
f_{n,i}\end{array} \right]+
\left[ \begin{array}{cccc}
\frac{\partial f_{1,i}}{\partial x_{1}} & \frac{\partial f_{1,i}}{\partial x_{2}} &
\cdots & \frac{\partial f_{1,i}}{\partial x_{n}} \\
\frac{\partial f_{2,i}}{\partial x_{1}} & \frac{\partial f_{2,i}}{\partial x_{2}} &
\cdots & \frac{\partial f_{2,i}}{\partial x_{n}} \\
\vdots & \vdots & & \vdots \\
\frac{\partial f_{n,i}}{\partial x_{1}} & \frac{\partial f_{n,i}}{\partial x_{2}} &
\cdots & \frac{\partial f_{n,i}}{\partial x_{n}} \\
\end{array} \right]
\left( \left[ \begin{array}{c}
x_{i+1} \\
x_{i+1} \\
\vdots \\
x_{i+1}\end{array} \right]-
\left[ \begin{array}{c}
x_{1,i} \\
x_{2,i} \\
\vdots \\
x_{n,i}\end{array} \right]\right)$
### Solution is again in the form Ax=b
$[J]([x_{i+1}]-[x_{i}])=-[f]$
so
$[x_{i+1}]= [x_{i}]-[J]^{-1}[f]$
## Example of Jacobian calculation
### Nonlinear springs supporting two masses in series
Two springs are connected to two masses, with $m_1$=1 kg and $m_{2}$=2 kg. The springs are identical, but they have nonlinear spring constants, of $k_1$=100 N/m and $k_2$=-10 N/m
We want to solve for the final position of the masses ($x_1$ and $x_2$)
$m_{1}g+k_{1}(x_{2}-x_{1})+k_{2}(x_{2}-x_{1})^{2}+k_{1}x_{1}+k_{2}x_{1}^{2}=0$
$m_{2}g-k_{1}(x_{2}-x_{1})-k_{2}(x_2-x_1)^{2}=0$
$J(1,1)=\frac{\partial f_{1}}{\partial x_{1}}=-k_{1}-2k_{2}(x_{2}-x_{1})+k_{1}+2k_{2}x_{1}$
$J(1,2)=\frac{\partial f_1}{\partial x_{2}}=k_{1}+2k_{2}(x_{2}-x_{1})$
$J(2,1)=\frac{\partial f_2}{\partial x_{1}}=k_{1}+2k_{2}(x_{2}-x_{1})$
$J(2,2)=\frac{\partial f_2}{\partial x_{2}}=-k_{1}-2k_{2}(x_{2}-x_{1})$
```octave
m1=1; % kg
m2=2; % kg
k1=100; % N/m
k2=-10; % N/m^2
```
```octave
function [f,J]=mass_spring(x)
% Function to calculate function values f1 and f2 as well as Jacobian
% for 2 masses and 2 identical nonlinear springs
m1=1; % kg
m2=2; % kg
k1=100; % N/m
k2=-10; % N/m^2
g=9.81; % m/s^2
x1=x(1);
x2=x(2);
J=[-k1-2*k2*(x2-x1)-k1-2*k2*x1,k1+2*k2*(x2-x1);
k1+2*k2*(x2-x1),-k1-2*k2*(x2-x1)];
f=[m1*g+k1*(x2-x1)+k2*(x2-x1).^2-k1*x1-k2*x1^2;
m2*g-k1*(x2-x1)-k2*(x2-x1).^2];
end
```
```octave
[f,J]=mass_spring([1,0])
```
f =
-190.19
129.62
J =
-200 120
120 -120
```octave
x0=[3;2];
[f0,J0]=mass_spring(x0);
x1=x0-J0\f0
ea=(x1-x0)./x1
[f1,J1]=mass_spring(x1);
x2=x1-J1\f1
ea=(x2-x1)./x2
[f2,J2]=mass_spring(x2);
x3=x2-J2\f2
ea=(x3-x2)./x3
x=x3
for i=1:3
xold=x;
[f,J]=mass_spring(x);
x=x-J\f;
ea=(x-xold)./x
end
```
x1 =
-1.5142
-1.4341
ea =
2.9812
2.3946
x2 =
0.049894
0.248638
ea =
31.3492
6.7678
x3 =
0.29701
0.49722
ea =
0.83201
0.49995
x =
0.29701
0.49722
ea =
0.021392
0.012890
ea =
1.4786e-05
8.9091e-06
ea =
7.0642e-12
4.2565e-12
```octave
x
X0=fsolve(@(x) mass_spring(x),[3;5])
```
x =
0.30351
0.50372
X0 =
0.30351
0.50372
```octave
[X,Y]=meshgrid(linspace(0,10,20),linspace(0,10,20));
[N,M]=size(X);
F=zeros(size(X));
for i=1:N
for j=1:M
[f,~]=mass_spring([X(i,j),Y(i,j)]);
F1(i,j)=f(1);
F2(i,j)=f(2);
end
end
mesh(X,Y,F1)
xlabel('x_1')
ylabel('x_2')
colorbar()
figure()
mesh(X,Y,F2)
xlabel('x_1')
ylabel('x_2')
colorbar()
```
![svg](lecture_13_files/lecture_13_36_0.svg)
![svg](lecture_13_files/lecture_13_36_1.svg)
```octave
```